How to Find the Greatest Common Divisor (GCD) in Python 🐍

by

Find the Greatest Common Divisor (GCD) in Python

The Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), is an important concept in mathematics and computer science. It’s the largest number that divides two or more integers without leaving a remainder. In Python, there are multiple ways to calculate the GCD, including using loops and built-in functions. In this blog, we’ll explore how to find the GCD of two numbers using Python.

By the end of this post, you’ll learn:

  • What the GCD of two numbers is.
  • How to calculate the GCD using Python’s built-in function.
  • How to calculate the GCD using Euclid’s Algorithm.

What is the Greatest Common Divisor (GCD)?

The GCD of two or more integers is the largest number that divides each of them exactly (without leaving a remainder). For example:

  • The GCD of 8 and 12 is 4, because 4 is the largest number that divides both 8 and 12.
  • The GCD of 54 and 24 is 6.

Formula for GCD

If you have two numbers a and b, the GCD is the largest integer d such that:


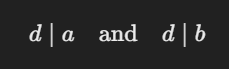
Where ( d \mid a ) means “d divides a” (i.e., there’s no remainder when a is divided by d).

How to Find the GCD in Python

There are two common methods to find the GCD in Python:

  1. Using Python’s built-in math.gcd() function.
  2. Using Euclid’s Algorithm, which is an efficient way to calculate the GCD.

Method 1: Using Python’s Built-in math.gcd() Function

Python’s math module provides a built-in function called gcd() that can quickly compute the GCD of two numbers.

# Program to find the GCD of two numbers using math.gcd

import math

# Step 1: Take user input
a = int(input("Enter the first number: "))
b = int(input("Enter the second number: "))

# Step 2: Find the GCD using math.gcd
gcd = math.gcd(a, b)

# Step 3: Display the result
print(f"The GCD of {a} and {b} is {gcd}")

Explanation of the Code

  1. Import the math module:
  • We import the math module, which provides access to mathematical functions in Python.
  1. User Input:
  • We take two integers a and b from the user using int(input()).
  1. Use the gcd() function:
  • math.gcd(a, b) returns the GCD of a and b.
  1. Display the Result:
  • The result is printed using an f-string: f"The GCD of {a} and {b} is {gcd}".

Sample Output

Enter the first number: 48
Enter the second number: 18
The GCD of 48 and 18 is 6

In this example, the GCD of 48 and 18 is 6.

Method 2: Using Euclid’s Algorithm

Euclid’s Algorithm is an efficient way to compute the GCD of two numbers. The algorithm is based on the principle that the GCD of two numbers doesn’t change if the larger number is replaced by the remainder when it’s divided by the smaller number. The process is repeated until one of the numbers becomes zero.

Here’s how Euclid’s Algorithm works:

  1. If b == 0, the GCD is a.
  2. Otherwise, set a = b and b = a % b, then repeat the process until b becomes zero.

Step-by-Step Guide for Euclid’s Algorithm

# Program to find the GCD of two numbers using Euclid's Algorithm

# Step 1: Take user input
a = int(input("Enter the first number: "))
b = int(input("Enter the second number: "))

# Step 2: Implement Euclid's Algorithm
def find_gcd(a, b):
    while b != 0:
        a, b = b, a % b  # Swap a with b, and b with a % b
    return a

# Step 3: Find the GCD
gcd = find_gcd(a, b)

# Step 4: Display the result
print(f"The GCD of {a} and {b} is {gcd}")

Explanation of the Code

  1. User Input:
  • We take two integers a and b from the user.
  1. Euclid’s Algorithm:
  • We define a function find_gcd(a, b) that implements Euclid’s Algorithm.
  • Inside the function, a while loop continues until b becomes 0. In each iteration, a is replaced by b, and b is replaced by a % b (the remainder).
  • When b == 0, the GCD is stored in a.
  1. Display the Result:
  • The result is printed using an f-string.

Sample Output

Enter the first number: 54
Enter the second number: 24
The GCD of 54 and 24 is 6

In this example, Euclid’s Algorithm calculates that the GCD of 54 and 24 is 6.

Understanding Euclid’s Algorithm

Let’s break down the steps for find_gcd(54, 24):

  1. First, calculate the remainder of 54 ÷ 24, which is 54 % 24 = 6.
  2. Next, we replace 54 with 24, and 24 with 6. The new pair is 24 and 6.
  3. Now, calculate 24 % 6 = 0. Since the remainder is 0, the GCD is 6.

Euclid’s Algorithm is efficient because it repeatedly reduces the size of the numbers involved, and it works even for large numbers.

Real-Life Applications of GCD

The GCD has several real-world applications:

  • Simplifying Fractions: The GCD can be used to reduce fractions to their simplest form. For example, ( \frac{18}{24} ) simplifies to ( \frac{3}{4} ) by dividing both the numerator and denominator by their GCD, which is 6.
  • Cryptography: The GCD plays an important role in number theory and cryptography, especially in algorithms like RSA.
  • Problem Solving: GCD is widely used in mathematical problem solving, especially when dealing with ratios, proportions, and divisibility.

Conclusion

In this blog, we explored two methods to find the GCD of two numbers in Python: using the built-in math.gcd() function and implementing Euclid’s Algorithm. Both methods are simple and efficient, but Euclid’s Algorithm offers a deeper understanding of how the GCD works mathematically. Whether you’re simplifying fractions or solving number theory problems, understanding the GCD is a fundamental skill in programming.

Would you like to see more Python tutorials? Stay tuned for more hands-on coding challenges and solutions! 😊

Share with our team

Leave a Comment