Compound interest is one of the most widely used financial concepts and is crucial for understanding investments, loans, and savings. In this blog, we will explore how to calculate compound interest in Python using a simple mathematical formula.
What is Compound Interest?
Compound interest is calculated on the initial principal and also on the accumulated interest of previous periods. Unlike simple interest, where interest is only calculated on the principal, compound interest allows your interest to earn interest over time, which can lead to significantly larger returns or interest owed.
The formula for calculating compound interest is:
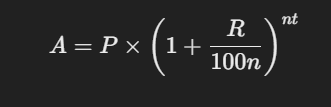
Where:
- A = Final amount (including interest)
- P = Principal amount (initial investment or loan)
- R = Annual interest rate (in percentage)
- n = Number of times interest is compounded per year
- t = Time period in years
To get the Compound Interest (CI), we subtract the principal from the final amount:
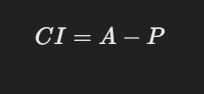
Steps to Write the Program
- Input the Principal, Rate of Interest, Time, and Compounding Frequency: We will prompt the user to input these values.
- Apply the Compound Interest Formula: Using the formula mentioned above, we will calculate the final amount and then derive the compound interest.
- Display the Result: Finally, we will print the compound interest and the total amount.
Python Program to Calculate Compound Interest
# Python program to calculate compound interest
# Input: Asking the user to enter the principal, rate of interest, time, and number of times compounded annually
P = float(input("Enter the principal amount: "))
R = float(input("Enter the rate of interest: "))
T = float(input("Enter the time period in years: "))
n = int(input("Enter the number of times the interest is compounded per year: "))
# Calculate the compound interest using the formula
A = P * (1 + (R / (100 * n))) ** (n * T) # Final amount after interest
CI = A - P # Compound interest is the final amount minus the principal
# Output: Display the compound interest and the final amount
print(f"The Compound Interest is: {CI}")
print(f"The Total Amount after interest is: {A}")Explanation:
- Input:
P: The initial investment or loan amount (principal).R: The annual interest rate as a percentage.T: The number of years the money is invested or borrowed for.n: The number of times that interest is compounded per year (e.g., annually, quarterly, monthly, etc.).
- Calculation:
- We calculate the final amount (A) using the compound interest formula.
- The compound interest (CI) is then derived by subtracting the principal (
P) from the final amount (A).
- Output:
- The result includes both the compound interest and the total amount after the interest is applied.
Sample Output
Test Case 1: Compounded Annually
Enter the principal amount: 5000
Enter the rate of interest: 5
Enter the time period in years: 2
Enter the number of times the interest is compounded per year: 1
The Compound Interest is: 512.5
The Total Amount after interest is: 5512.5Test Case 2: Compounded Quarterly
Enter the principal amount: 10000
Enter the rate of interest: 4
Enter the time period in years: 3
Enter the number of times the interest is compounded per year: 4
The Compound Interest is: 1265.3196772539175
The Total Amount after interest is: 11265.319677253918Understanding the Formula
The compound interest formula involves a few key concepts:
- Principal (P): The initial amount that is either invested or borrowed.
- Rate of Interest (R): The annual interest rate (in percentage) that applies to the principal.
- Compounding Frequency (n): The number of times the interest is applied in a year (e.g., if it’s compounded quarterly, then
n = 4). - Time (T): The total time in years for which the interest will be applied.
The main difference between compound and simple interest is that compound interest is calculated on both the initial principal and accumulated interest, leading to faster growth or larger interest payments.
Handling Edge Cases
- Negative or Zero Values:
- If any input values (Principal, Rate, Time, or n) are zero or negative, the program will still compute the result as per the formula, though it might not make sense in real-world financial scenarios. Example:
Enter the principal amount: 0
Enter the rate of interest: 5
Enter the time period in years: 2
Enter the number of times the interest is compounded per year: 1
The Compound Interest is: 0.0
The Total Amount after interest is: 0.0- Decimal Values:
- The program can handle decimal values for both the rate of interest and time period. This is useful in real-world scenarios where interest rates may have fractional values, and the time period may not be a whole number. Example:
Enter the principal amount: 2000
Enter the rate of interest: 4.5
Enter the time period in years: 2.5
Enter the number of times the interest is compounded per year: 12
The Compound Interest is: 242.823
The Total Amount after interest is: 2242.823Enhancing the Program with Exception Handling
To make the program more robust and prevent invalid inputs, you can add a try-except block for error handling:
# Python program to calculate compound interest with error handling
try:
# Input: Asking the user to enter the principal, rate of interest, time, and number of times compounded annually
P = float(input("Enter the principal amount: "))
R = float(input("Enter the rate of interest: "))
T = float(input("Enter the time period in years: "))
n = int(input("Enter the number of times the interest is compounded per year: "))
# Calculate the compound interest using the formula
A = P * (1 + (R / (100 * n))) ** (n * T)
CI = A - P
# Output: Display the compound interest and the final amount
print(f"The Compound Interest is: {CI}")
print(f"The Total Amount after interest is: {A}")
except ValueError:
print("Invalid input! Please enter numeric values for principal, rate, time, and compounding frequency.")Now, if a user enters non-numeric values or any invalid input, the program will catch the error and display a user-friendly message.
Conclusion
Calculating compound interest is an essential concept in personal finance, loans, and investments. With the help of this Python program, you can easily calculate compound interest for various investment or loan scenarios.
The compound interest formula allows for calculating interest that accumulates over time, leading to faster growth compared to simple interest. This Python program demonstrates how to implement the formula in code, accepting user inputs and displaying the correct results.
In this blog, we also covered how to handle edge cases and how to improve the program with exception handling to make it more robust.
By mastering how to calculate compound interest, you’re not only improving your Python skills but also gaining a fundamental understanding of finance. Keep practicing and applying your knowledge to more complex real-world problems! Happy coding!